検証: レバレッジ型ETFへの長期投資
2022年06月30日
昨年6月、金融庁はレバレッジ型上場投資信託(レバレッジ型ETF)などに関する説明義務を強化した。レバレッジ型ETFとは、株価指数、商品指数、為替レートといった指標の日次変動率の一定倍をリターンとして提供することを目指すETFである。義務の強化に当たって金融庁が示した説明は、義務そのものよりずっと興味深い。曰く、レバレッジ型ETFは、
「2日以上の期間では、変動率が2倍とならないため、中長期的に価値が逓減する可能性が高いため長期保有に不向き」
ここには命題が3つ入っている。それぞれみていこう。
命題①: 2日以上の期間では、変動率が2倍とならない
この命題を端的に示すべく運用業界でよく使われた数値例に「指数が10%上がって10%下がったらどうなるか」がある。2倍のレバレッジ(以下、2倍指数)なら次の通りだ。
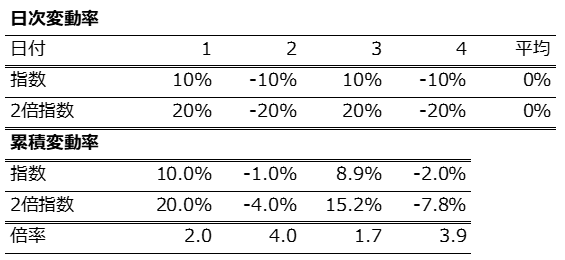
たしかに2日以上の期間では変動率は2倍となっていない。
命題②: 中長期的に価値が逓減する可能性が高い
上記の例だと平均リターンは0%なのに2倍指数の累積変動率はマイナスになっており、つまり「価値は逓減」している。しかし、それは元の「指数」も同じで、価値が逓減するのはレバレッジのせいではないのがわかる。これは次の関係に基づく。
算術平均≧幾何平均
中学の算数でいえば相加平均≧相乗平均だ。変動する日次リターンの算術平均が0なら幾何平均は0を下回る。リスクがあって長期の期待リターンがマイナスの資産など、レバレッジ以前に誰も買いたくないだろう。この数値例はレバレッジ型投資信託が短期投資向けだとする根拠によく使われてきたが、適切な例とはいいがたいのではないか。
命題③: 長期保有には向かない
リターンの算術平均と幾何平均の間には、近似的に
幾何平均(g)≒算術平均(μ)-分散(σ²)/2
が成り立つ。L: レバレッジの大きさ(>1)として指数の長期保有を考えるとき、
a)μ-σ²/2 > 0: その指数は上昇すると期待できる。
b)μ-Lσ²/2 > 0: その指数にL倍のレバレッジをかけた指標は上昇すると期待できる。つまり「レバレッジ指数」は逓増する可能性が高い。
c)μ-(L+1)σ²/2 > 0: 指数をそのまま持つよりレバレッジ指数のほうが期待将来価値は大きい、つまりレバレッジ指標がより上昇すると期待できる。
株価指数でよく使われる期待リターン年率6%、標準偏差年率20%を日次に変換して計算するとa)は成り立ち、レバレッジが2倍ならb)とc)がいずれも成り立ち、3倍だとb)は成り立ってもc)は成り立たない。株式のレバレッジ型ETFに2倍が多いのはそういう理由かもしれない。
ちなみに命題①もやはり間違いで、期間あたりのリターンがプラスなら累積リターンは時間とともに指数級数的に累積する。線形ではないので、短期でのリターン格差が小さくても、長期では格差は累積して、たとえば「2倍」にでも、あるいは1を上回る任意のx倍にでも、到達すると期待できる。
まとめ
レバレッジ型ETFの長期収益率は、元の指数の長期収益率だけでなく、リスクがどれだけかも見積もらないとわからない。それができる投資家だけがレバレッジをかけて長期投資に臨むに値する。その意味で説明義務の強化は正しい。でも根拠のほうはどうだろう。
このコンテンツの著作権は、株式会社大和総研に帰属します。著作権法上、転載、翻案、翻訳、要約等は、大和総研の許諾が必要です。大和総研の許諾がない転載、翻案、翻訳、要約、および法令に従わない引用等は、違法行為です。著作権侵害等の行為には、法的手続きを行うこともあります。また、掲載されている執筆者の所属・肩書きは現時点のものとなります。
関連のレポート・コラム
最新のレポート・コラム
-
人手不足時代の外国人労働者の受け入れと共生の課題
潜在成長率を年率0.4%pt押し上げ/共生の鍵は日本語教育
2026年02月26日
-
テキスト分析が映し出す金融当局の楽観視
金融当局ネガティブ指数で、金融システムへの警戒感の変化を読む
2026年02月26日
-
ガバナンス・コードはスリム化するか?
原則の統合によって原則数減少、独立性判断方針の「策定・開示」から「策定」へ変更し要開示事項が減少
2026年02月26日
-
高市政権の消費減税と成長戦略を検証する
成長投資・危機管理投資に求められる「選択と集中」
2026年02月26日
-
有価証券届出書の提出免除基準の引上げと残された課題
2026年02月25日





